Vous n'êtes pas identifié.
Annonce
Bienvenue sur le site support de mes ouvrages d'introduction à SAS
La 4ème édition de mon ouvrage est toujours disponible !
Attention, pour vous inscrire ou poster dans le forum de discussions, vous devez impérativement accéder à ce site via https://www.sas-sr.com
Pages: 1
- Accueil forums
- » Les beaux mercredis !
- » [archive] Liliane, fais les valises, on rentre à Paris
#1 20-06-2019 06:19:22
[archive] Liliane, fais les valises, on rentre à Paris
ou le modèle de ségrégation de Schelling
Le titre de ce sujet des beaux mercredis a peu de chance de faire rire les moins de 50 ans....
https://www.youtube.com/watch?v=x_NihRC7W0s
bref...
Mon collègue de bureau a récemment attiré mon attention sur cette page du site de Thomas J. Sargent et John Stachurski "Quantitative Economics with Python".
https://lectures.quantecon.org/py/schelling.html
et là vous vous dites "quoi ! on fait du python sur www.sas-sr.com ? tout fout le camp..."
mais non, je vous rassure tout de suite mais le sujet que Sargent et Stachurski traite est tout à fait intéressant !
Schelling (prix nobel 1985) a développé un modèle très simple qui explique la formation des ghettos. Imaginons une ville dans laquelle vous avez deux types de population : les rouges et les bleus. Une personne est heureuse si, parmi ses 10 voisins les plus proches, il y a au moins 5 personnes du même type qu'elle.
S'il n'y a que 4 personnes ou moins qui lui ressemble, la personne va déménager et au bout de quelques périodes, on constate que des ghettos rouge et bleu se forment.
L'objectif de Sargent et Stachurski est de proposer un programme en python qui montre la formation de ces ghettos.
Si on peut le faire en python, on peut le faire en SAS... nous allons cependant légèrement modifier leur approche.
Ils vous disent : imaginons une ville contenant 250 verts et 250 oranges. Notre ville contiendra elle aussi 500 habitants mais le type (bleu/rouge) sera déterminé au hasard.
La ville de Sargent et Stachurski, tout comme la notre, est en fait un carré de 1*1 et la position de chaque habitant (x ; y) avec 0<x<1 et 0<y<1, est tirée au hasard.
la distance qui sépare chaque habitant est une distance euclidienne et, comme nous l'avons dit plus haut, un habitant est heureux s'il a au moins, parmi ses 10 voisins les plus proches, au moins 5 voisins du même type que lui : il est identiquement heureux si 10, 9, 8, 7, 6 ou 5 voisins sont identiques à lui (et donc peut être parfaitement heureux s'il a jusqu'à 5 voisins différents de lui) : il n'y a pas d'aversion à vivre dans un environnement mixte.
Quand l'individu n'est pas heureux, il déménage. Sargent et Stachurski indiquent qu'il va déménager vers un endroit où il pourrait être heureux, nous allons ici procéder différemment en considérant que l'individu déménage "au hasard" : lorsque je déménage, je ne choisis pas de moi même d'aller dans un ghetto.
Sargent et Stachurski montrent qu'en quelques cycles, on aboutit à un équilibre stable (dans lequel plus personne ne souhaite déménager) : la "carte" de la ville vous montre que c'est au prix de la formation de ghettos, zones peu mixtes.
comment montrer cela avec SAS ?
Construisons une ville et plaçons y 500 habitants rouge/bleu au hasard :
le nombre d'habitants de la ville est saisi dans une macro variable. Si l'envie nous prend de construire une ville avec un nombre différent d'habitants, nous n'aurons qu'à changer la valeur de la macro variable NB.
Code:
%let nb=500 ;
data loc(keep=x: y: type:) ;
array type(&nb);
array x(&nb);
array y(&nb);
do i=1 to &nb;
type(i)=round(rand("uniform"),1);
x(i)=rand("uniform");
y(i)=rand("uniform");
end;
run;voilà, c'est fait : on dispose d'une table d'une observation et 1500 variables : X1 et Y1 vous donne la position du premier individu, TYPE1 vous donne son type. X2 et Y2 donne la position du second individu, son type est renseigné par TYPE2, etc.
Vous pouvez dès maintenant faire une première "carte de la ville". On va partir de la table LOC mais allons devoir la "transposer par partie" avant de réunir ces parties afin de disposer d'un table contenant trois variables pouvant être mobilisées par PROC SGPLOT et SCATTER.
Code:
proc transpose data=loc(keep=x:) prefix=X out=lac1; run; proc transpose data=loc(keep=y:) prefix=y out=lac2; run; proc transpose data=loc(keep=type:) prefix=t out=lac3; run; data lac4; merge lac1 lac2 lac3; run; ods graphics / width=600 height=600; title "la carte initiale"; proc sgplot data=lac4 noautolegend ; scatter x=x1 y=y1 / group=t1 markerattrs=(symbol=circlefilled size=8pt); xaxis display=(nolabel); yaxis display=(nolabel); run;
et on obtient :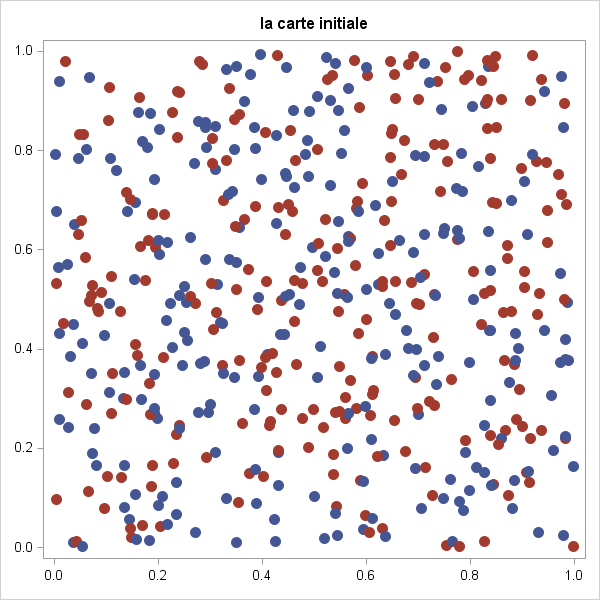
La semaine prochaine, à partir de cet état initial de la ville, nous verrons comment construire trois nouvelles séries de variables :
- des variables DIST qui vont mesurer les distances qui me séparent de mes voisins
- des variables SAME qui indiqueront combien de voisins identiques à moi j'ai parmi mes 10 voisins les plus proches
- des variables MOVE qui vont indiquer si je vais déménager ou pas...
à suivre
Ce sujet est maintenant archivé - seuls les utilisateurs inscrits de www.sas-sr.com peuvent consulter l'intégralité du sujet et les réponses aux questions posées.
pour vous identifier, suivez ce lien
pour vous inscrire, suivez ce lien
Hors ligne
Pages: 1
- Accueil forums
- » Les beaux mercredis !
- » [archive] Liliane, fais les valises, on rentre à Paris

 Flux RSS
Flux RSS